Apakah sekolah di program doktor berpengaruh ke keluarga?
Recent newsLatar belakang kenapa hal ini menjadi kegundahan.
Pertama tama yang harus dicamkan di sini adalah, sekolah doktor seperti halnya dengan pekerjaan pada umumnya, mereka membutuhkan waktu spesial untuk anda fokus. Dedikasi fokus ini seperti halnya pekerjaan, juga tentu berimpak pada waktu anda ke keluarga. Dan hal ini berimpak juga pada waktu yang anda habiskan ke istri / suami, anak, orang tua dan sebagainya.
read more

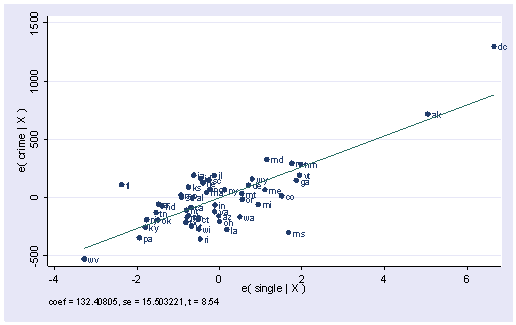
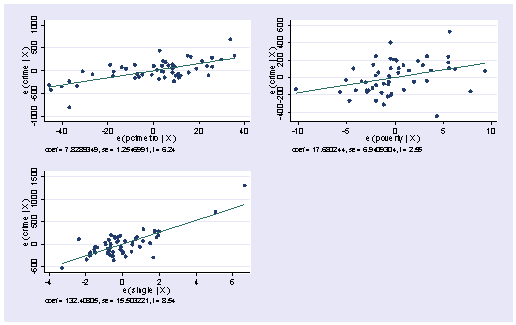
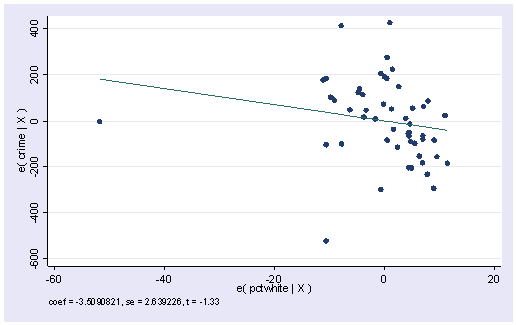




Comments