Mixed-Effect Modeling using MATLAB
Linear Mixed-Effect (LME) Models are generalizations of linear regression models for data that is collected and summarized in groups. Linear Mixed- Effects models offer a flexible framework for analyzing grouped data while accounting for the within-group correlation often present in such data.
This example illustrates how to fit basic hierarchical or multilevel LME models.
Copyright (c) 2014, MathWorks, Inc.
Contents
- Description of the Data
- Load Data
- Preprocess Data
- Fit a linear model and visualize the Gross State Product by region
- Visualize data and fitted model
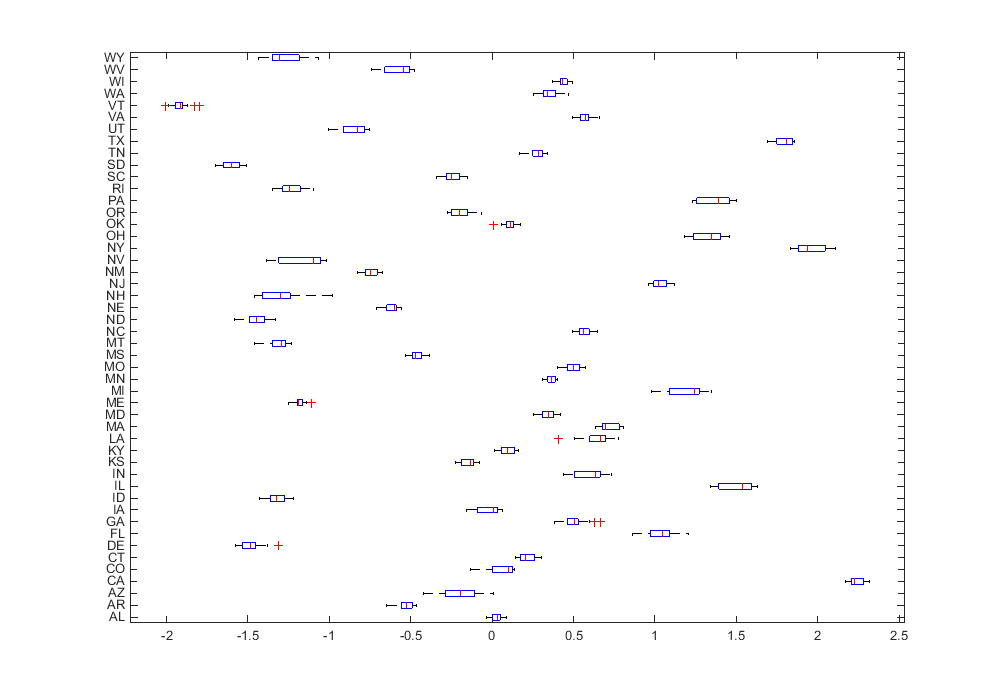
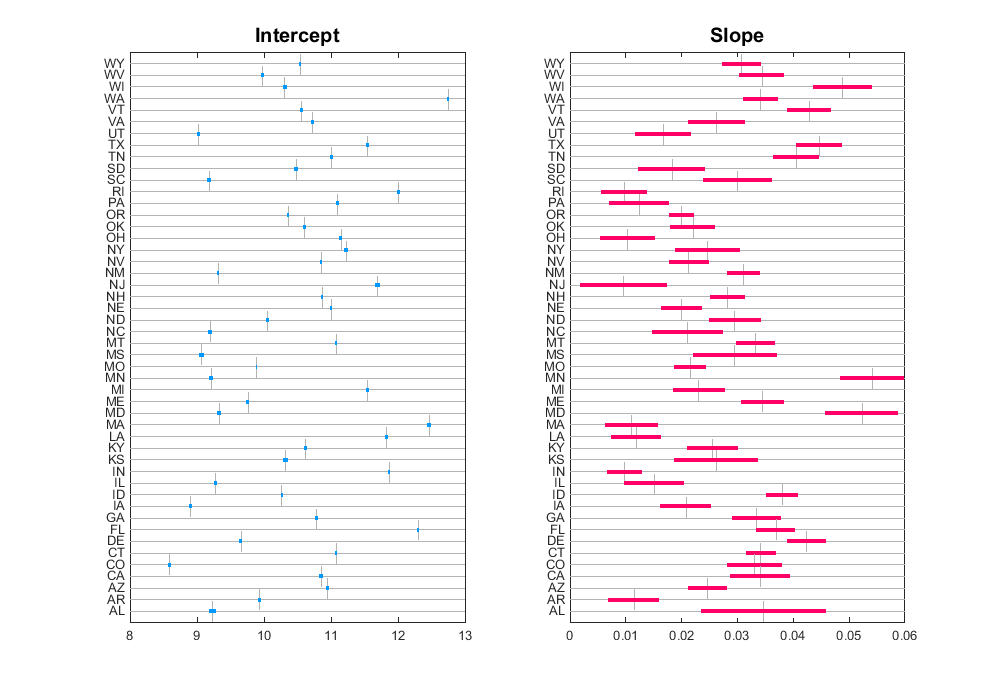
- Fit separate linear models per group and visualize intervals of parameters
- Fit a single linear model with dummy variables for each state
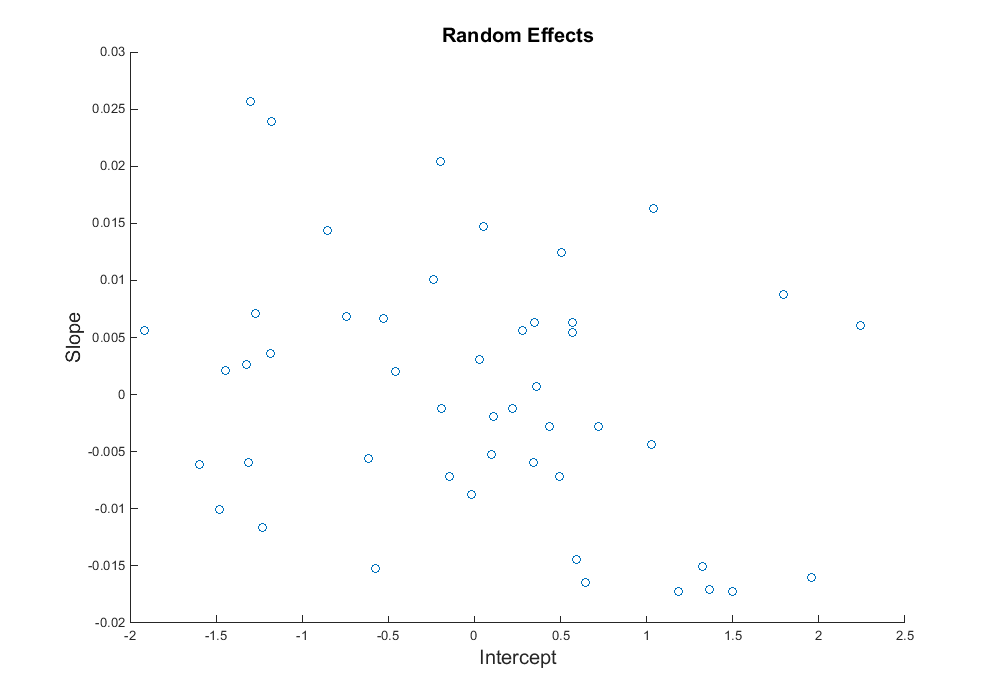
- Fit a random intercept model
- Fit a random intercept and slope model
- Compare random slope and intercept models using Likelihood Ratio Test
- Fit Mixed-Effect models using matrix notation
- Forecast state GDP
Description of the Data
This dataset consists of annual observations of 48 Continental U.S. States, over the period 1970–86 (17 years). This data set was provided by Munnell (1990)
- GDP: Gross Domestic Product by state (formerly Gross State Product)
- STATE: Categorical variable indicating the state
- YR: Year the GDP value was recorded
Reference:
- Munnell AH (1990). Why Has Productivity Growth Declined? Productivity and Public Investment.” New England Economic Review
- Econometric Analysis of Panel Data, 5th Edition, Badi H. Baltagi
Load Data
clear, clc, close all
loadPublicData
If you don't have the data. You can download the Zip file from here.
Preprocess Data
Convert STATE, YR and REGION to categorical, In Matlab 2021, its appear as a default that you will get it as a categorical
publicdata.STATE = categorical(publicdata.STATE);
% Compute log(GDP)
publicdata.log_GDP = log(publicdata.GDP);
publicdata.GDP = [];
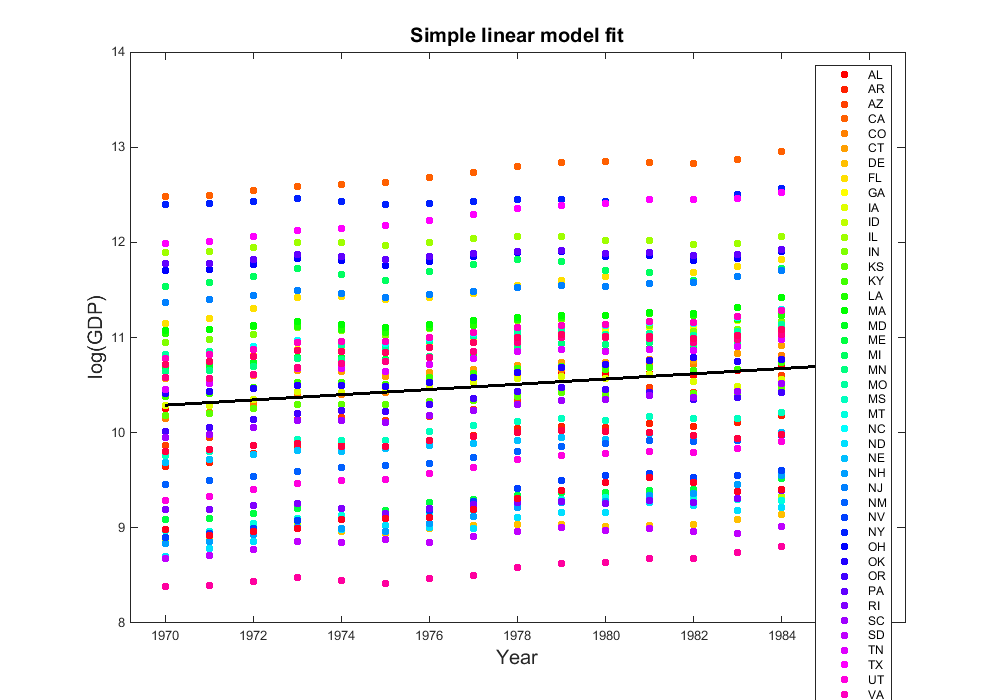
Fit a linear model and visualize the Gross State Product by region
The formula is
\( log\_GDP_i = \beta_0 + \beta_1 YR_i + \epsilon_i \)













Comments