Mixed-Effect Modeling using MATLAB
Mixed-Effect Modeling for Panel DataMixed-Effect Modeling for Panel Data
Panel Data refers to observations on a cross-section (of individuals, households, firms, municipalities, states or countries) that are repeated over time (five-year intervals, annual, quarters, weeks, days) Due to the nature of the data we cannot assume that the observations are independently distributed across time.
This example introduces fitting different types of Panel Regression models using Mixed-Effect modelling techniques.
Copyright (c) 2014, MathWorks, Inc.
Contents
- Description of the Data
- Load Data
- Preprocess Data
- Balanced and Unbalanced Panel
- Cobb–Douglas production function
- Ordinary Least Squares (OLS) Model
- Fixed-Effects Model
- One-Way Random effects Model (Mixed-Effect Model)
- One-Way Random Effects Model with different predictors
- Compare the two One-Way Random Effects models for improvements
- Two-Way Random effects Model (Mixed-Effect Model)
- Multilevel (Hierarchical) Model: STATE nested in REGION
- Regional random effects for UNEMP and HWY with possible correlation
- Table showing Cobb–Douglas Production Function Estimates for different models
- Bibliography
Description of the Data
This panel consists of annual observations of 48 Continental U.S. States, over the period 1970–86 (17 years). Panel data allows you to control for variables you cannot observe. Examples are cultural factors or differences in business practices across companies; or variables that change over time but not across entities (i.e. national policies, federal regulations, international agreements, etc.). That is, it accounts for individual heterogeneity. This data set was provided by Munnell (1990)
- GDP: Gross State Product by state, Bureau of Economic Analysis
- PUB_CAP: Public capital which includes (HWY, WATER, UTIL)
- HWY: Highways and streets capital stock
- WATER: Water and sewer facilities capital stock
- UTIL: Other public buildings and structures capital stock
- PVT_CAP: Private capital stock based on the Bureau of Economic Analysis national stock estimates
- EMP: Employees on non-agricultural payrolls, Bureau of Labor Statistics
- UNEMP: Unemployment Rate, included capturing business cycle effects, Bureau of Labor Statistics
All dollar figures are millions; the employment figure is in thousands Reference:
STATE and REGION data
- GF = Gulf =AL, FL, LA, MS,
- MW = Midwest =IL, IN, KY, Ml, MN, OH, Wl,
- MA = Mid Atlantic =DE, MD, NJ, NY, PA, VA,
- MT = Mountain =CO, ID, MT, ND, SD, WY,
- NE = New England=CT, ME, MA, NH, RI, VT,
- SO = South =GA, NC, SC, TN, WV, R,
- SW = Southwest =AZ, NV, NM, TX, UT,
- CN = Central =AK, IA, KS, MO, NE, OK,
- WC = West Coast =CA, OR, WA.
Load Data
clear, clc, close all
loadPanelData
Preprocess Data
Convert STATE, YR and REGION to categorical
publicdata.STATE = categorical(publicdata.STATE); publicdata.REGION = categorical(publicdata.REGION); publicdata.YR = categorical(publicdata.YR);
For this Panel Regression example, we will fit the famous Cobb–Douglas production function which uses the log transform of the following variables: GDP, PUB_CAP, PC and EMP
logvars = {'PUB_CAP','HWY','WATER','UTIL','PVT_CAP','EMP','GDP'};
publicdata = [publicdata varfun(@log,publicdata(:,logvars))];
publicdata(:,logvars) = [];
clear logvars
Balanced and Unbalanced Panel
The Panel Dataset we are working with is a balanced or complete panel. This means that all observations for each state are measured at the same time points (1970 - 1986). If the GDP is unstacked with STATE as the indicator variable and observed over time, notice that there are no missing values.
unstacked = unstack(publicdata,'log_GDP','STATE',... 'GroupingVariable','YR');
If we randomly remove certain observations from the data and unstack GDP we now notice missing information which is not clear when observing the stacked panel.
publicdata_missing_years = publicdata; publicdata_missing_years(randperm(100,20),:) = []; % An alternative way to visualize the same data is to unstack the panel unstacked_missing = unstack(publicdata_missing_years,... 'log_GDP','STATE','GroupingVariable','YR'); unstacked_missing = sortrows(unstacked_missing,'YR','ascend');
Unbalanced or incomplete panels can occur if some states have data going back several more years than others or some states don't have recorded observations for certain years. fitlme can fit both types of panels. Because Random Effects are assumed to come from a common distribution, Mixed-Effects models share information between groups. This can improve the precision of predictions for groups that have fewer data points.
Cobb–Douglas production function
Model the production function relationship investigating the productivity of public capital in private production as proposed by Munnell(1990):
\( log(GDP) = \beta_0 + \beta_1 UNEMP + \beta_2 log(PUB\_CAP) + \)
\( \beta_3 log(PVT\_CAP) + \beta_4 log(EMP) + \epsilon \)
Ordinary Least Squares (OLS) Model
An OLS model is also called Pooled OLS Regression since it combines the cross-section and time-series aspects of the data. It is sometimes referred to as a population-averaged model. The assumption here is that all statistical requirements of OLS are met.
lm_ols = fitlm(publicdata,... 'log_GDP ~ 1 + UNEMP + log_PUB_CAP + log_PVT_CAP + log_EMP')
lm_ols =
Linear regression model:
log_GDP ~ 1 + UNEMP + log_PUB_CAP + log_PVT_CAP + log_EMP
Estimated Coefficients:
Estimate SE tStat pValue
_________ _________ _______ ___________
(Intercept) 1.6433 0.057587 28.536 1.4849e-124
UNEMP -0.006733 0.0014164 -4.7537 2.3632e-06
log_PUB_CAP 0.15501 0.017154 9.0363 1.1674e-18
log_PVT_CAP 0.30919 0.010272 30.1 3.0988e-134
log_EMP 0.59393 0.013747 43.203 1.5408e-212
Number of observations: 816, Error degrees of freedom: 811
Root Mean Squared Error: 0.0881
R-squared: 0.993, Adjusted R-Squared: 0.993
F-statistic vs. constant model: 2.72e+04, p-value = 0
OLS reports that public capital is productive and economically significant in the state's private production (log_PUB_CAP: 0.155) and the p-Values show that the fit is statistically significant. Ignoring that the data is grouped by state. From the model, we can infer that at the state level, that public capital has a significant positive impact on the level of output and does indeed belong in the production function. However, it should be noted that pooled regression may lead to underestimated standard errors and inflated t-statistics. OLS assumes that the observation error is independent across observations. However, when the data is grouped as in this case, within-group observations are correlated with each other.
boxplot(lm_ols.Residuals.Raw,publicdata.STATE)
ylabel('OLS Residuals')

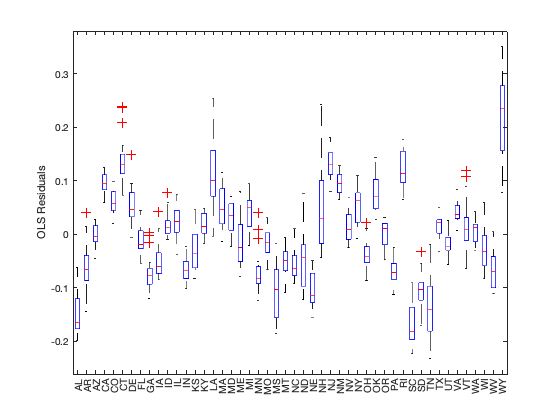
The boxplot of OLS residuals by STATE shows that the within state residuals are either all positive or all negative and are not centred at 0. This violates the fundamental assumption of OLS and the resulting inference may not be valid.
Fixed-Effects Model
Fixed-Effect models treat individual effects as fixed but unknown parameters, so as to allow the unobserved individual effects to be correlated with the included variables. Panel Data Fixed-Effect models also refer to Least Squares with Dummy Variables (LSDV) models. All the state-specific information is incorporated in the dummy variables. fitlm automatically does this under the hood, and it is ideal for fixed-effect models with a moderate number of cross-sectional units.
lm_fe = fitlm(publicdata,... 'log_GDP ~ 1 + UNEMP + log_PUB_CAP + log_PVT_CAP + log_EMP + STATE') disp(' '), disp(['log_PUB_CAP OLS Estimate: ', num2str(lm_ols.Coefficients{'log_PUB_CAP',1})]) disp(['log_PUB_CAP FE Estimate: ', num2str(lm_fe.Coefficients{'log_PUB_CAP',1})])
lm_fe =
Linear regression model:
log_GDP ~ 1 + STATE + UNEMP + log_PUB_CAP + log_PVT_CAP + log_EMP
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ ________ ___________
(Intercept) 2.2016 0.176 12.509 8.5462e-33
STATE_AR 0.061399 0.01672 3.6722 0.00025726
STATE_AZ 0.16647 0.013634 12.21 1.8928e-31
STATE_CA 0.29881 0.036815 8.1164 1.9175e-15
STATE_CO 0.19429 0.013746 14.135 1.8158e-40
STATE_CT 0.26959 0.018807 14.334 1.903e-41
STATE_DE 0.21184 0.022432 9.444 4.2496e-20
STATE_FL 0.13154 0.020489 6.4198 2.3943e-10
STATE_GA 0.056591 0.016073 3.521 0.00045546
STATE_IA 0.12555 0.014002 8.9666 2.3216e-18
STATE_ID 0.1368 0.025164 5.4363 7.3251e-08
STATE_IL 0.1857 0.024067 7.7161 3.7521e-14
STATE_IN 0.057766 0.014086 4.101 4.5557e-05
STATE_KS 0.1371 0.015636 8.7683 1.1666e-17
STATE_KY 0.19767 0.014 14.119 2.1724e-40
STATE_LA 0.31305 0.02213 14.146 1.6006e-40
STATE_MA 0.1606 0.02308 6.9586 7.3977e-12
STATE_MD 0.19866 0.020253 9.8092 1.7882e-21
STATE_ME 0.066799 0.025235 2.647 0.008287
STATE_MI 0.21538 0.02168 9.9344 5.9093e-22
STATE_MN 0.11393 0.016549 6.8845 1.2107e-11
STATE_MO 0.11201 0.015263 7.3384 5.5345e-13
STATE_MS 0.048408 0.014256 3.3955 0.00072041
STATE_MT 0.14654 0.026661 5.4962 5.2903e-08
STATE_NC 0.036009 0.016971 2.1217 0.03418
STATE_ND 0.14228 0.029669 4.7955 1.9508e-06
STATE_NE 0.10966 0.016396 6.6883 4.3605e-11
STATE_NH 0.12253 0.027357 4.479 8.6463e-06
STATE_NJ 0.24125 0.020144 11.977 2.0566e-30
STATE_NM 0.25276 0.022268 11.351 1.0563e-27
STATE_NV 0.14027 0.024615 5.6986 1.7244e-08
STATE_NY 0.27437 0.038809 7.0699 3.5037e-12
STATE_OH 0.12103 0.022762 5.3171 1.3856e-07
STATE_OK 0.21432 0.016437 13.039 3.1226e-35
STATE_OR 0.14929 0.013996 10.666 7.4331e-25
STATE_PA 0.087726 0.024799 3.5375 0.00042837
STATE_RI 0.18673 0.030334 6.1559 1.2049e-09
STATE_SC -0.082223 0.016847 -4.8806 1.2881e-06
STATE_SD 0.088063 0.023997 3.6697 0.00025968
STATE_TN 0.027481 0.015532 1.7693 0.077245
STATE_TX 0.19204 0.025172 7.6292 7.0358e-14
STATE_UT 0.12704 0.017077 7.4394 2.725e-13
STATE_VA 0.17885 0.018246 9.8022 1.9006e-21
STATE_VT 0.13458 0.028763 4.679 3.409e-06
STATE_WA 0.24516 0.020582 11.912 3.9728e-30
STATE_WI 0.12734 0.017036 7.475 2.1186e-13
STATE_WV 0.091533 0.018279 5.0077 6.8458e-07
STATE_WY 0.44694 0.039891 11.204 4.4053e-27
UNEMP -0.0052977 0.00098873 -5.3582 1.1139e-07
log_PUB_CAP -0.02615 0.029002 -0.90166 0.36752
log_PVT_CAP 0.29201 0.02512 11.625 7.0751e-29
log_EMP 0.76816 0.030092 25.527 2.0215e-104
Number of observations: 816, Error degrees of freedom: 764
Root Mean Squared Error: 0.0381
R-squared: 0.999, Adjusted R-Squared: 0.999
F-statistic vs. constant model: 1.14e+04, p-value = 0
log_PUB_CAP OLS Estimate: 0.15501
log_PUB_CAP FE Estimate: -0.02615
Notice that the output contains coefficient estimates for each state. In contrast to OLS, the LSDV model reports that public capital is not as economically significant (log_PUB_CAP: -0.02) However, disadvantages to this approach include loss in degrees of freedom when there are a large number of groups and therefore a large number of estimated fixed parameters. The complexity of this model then increases linearly with the number of STATEs. This can be a problem when dealing with a smaller set of observations.
One-Way Random effects Model (Mixed-Effect Model)
Group-specific effects can be modelled using random effects. The state-specific observations in this example are assumed drawn at random from a population. fitlme uses Maximum Likelihood (ML) or Restricted Maximum Likelihood (REML) estimation to compute the coefficients.
lme_oneway = fitlme(publicdata,... 'log_GDP ~ 1 + log_PUB_CAP + log_PVT_CAP + log_EMP + UNEMP + (1 | STATE)',... 'FitMethod','REML') disp(' ') disp(['log_PUB_CAP OLS Estimate: ', num2str(lm_ols.Coefficients{'log_PUB_CAP',1})]) disp(['log_PUB_CAP FE Estimate: ', num2str(lm_fe.Coefficients{'log_PUB_CAP',1})]) disp(['log_PUB_CAP RE Estimate: ', num2str(lme_oneway.Coefficients{3,2})])
lme_oneway =
Linear mixed-effects model fit by REML
Model information:
Number of observations 816
Fixed effects coefficients 5
Random effects coefficients 48
Covariance parameters 2
Formula:
log_GDP ~ 1 + UNEMP + log_PUB_CAP + log_PVT_CAP + log_EMP + (1 | STATE)
Model fit statistics:
AIC BIC LogLikelihood Deviance
-2750.7 -2717.8 1382.4 -2764.7
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF
{'(Intercept)'} 2.1493 0.1357 15.839 811
{'UNEMP' } -0.006116 0.00091025 -6.719 811
{'log_PUB_CAP'} 0.0023163 0.02365 0.097941 811
{'log_PVT_CAP'} 0.30933 0.020082 15.404 811
{'log_EMP' } 0.73241 0.025211 29.051 811
pValue Lower Upper
1.9677e-49 1.883 2.4157
3.4438e-11 -0.0079028 -0.0043293
0.922 -0.044106 0.048739
3.7475e-47 0.26991 0.34875
9.6728e-128 0.68292 0.78189
Random effects covariance parameters (95% CIs):
Group: STATE (48 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.087071
Lower Upper
0.070498 0.10754
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.038157 0.036289 0.04012
log_PUB_CAP OLS Estimate: 0.15501
log_PUB_CAP FE Estimate: -0.02615
log_PUB_CAP RE Estimate: 0.0023163
In contrast to OLS, a mixed-effect model with STATE specific random effect finds that public capital is economically insignificant in the state's private production (log_PUB_CAP: 0.0023).
Mixed-Effects models such as the one above are also known as error component models, random co-efficient regression models, covariance structure models, or multilevel models. The Statistics Toolbox follows the Mixed-Effects terminology, where the regression model consists of two separate parts, fixed effects and random effects. Fixed-effects terms are the conventional linear regression part, and the random effects are associated with group and are assumed to have a prior distribution.
One-Way Random Effects Model with different predictors
An important aspect of building an accurate predictive model it to choose the right set of predictors. We can attempt to improve the existing random-effects model by including HWY, WATER and UTIL as separate predictors instead of PUB_CAP.
Recall that PUB_CAP = HWY + WATER + UTIL
clc lme_oneway_new = fitlme(publicdata,... ['log_GDP ~ 1 + log_HWY + log_WATER + log_UTIL + log_PVT_CAP +'... 'log_EMP + UNEMP + (1 | STATE)'],'FitMethod','REML')
lme_oneway_new =
Linear mixed-effects model fit by REML
Model information:
Number of observations 816
Fixed effects coefficients 7
Random effects coefficients 48
Covariance parameters 2
Formula:
Linear Mixed Formula with 7 predictors.
Model fit statistics:
AIC BIC LogLikelihood Deviance
-2787.7 -2745.5 1402.9 -2805.7
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF
{'(Intercept)'} 2.1782 0.14939 14.581 809
{'UNEMP' } -0.0057842 0.00089788 -6.4421 809
{'log_HWY' } 0.062865 0.022921 2.7427 809
{'log_WATER' } 0.07543 0.014041 5.3722 809
{'log_UTIL' } -0.10099 0.01716 -5.8853 809
{'log_PVT_CAP'} 0.2694 0.020855 12.917 809
{'log_EMP' } 0.7557 0.025775 29.319 809
pValue Lower Upper
6.2342e-43 1.885 2.4715
2.0208e-10 -0.0075466 -0.0040218
0.0062284 0.017874 0.10786
1.0178e-07 0.047869 0.10299
5.8166e-09 -0.13468 -0.06731
7.7082e-35 0.22846 0.31033
2.6003e-129 0.70511 0.8063
Random effects covariance parameters (95% CIs):
Group: STATE (48 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.089868
Lower Upper
0.07251 0.11138
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.036808 0.035003 0.038706
The log_HWY, log_WATER and log_UTIL estimates are statistically significant. log_UTIL appears to have a negative economic impact on the states private capital.
Compare the two One-Way Random Effects models for improvements
clc compare(lme_oneway, lme_oneway_new)
ans =
THEORETICAL LIKELIHOOD RATIO TEST
Model DF AIC BIC LogLik LRStat deltaDF
lme_oneway 7 -2750.7 -2717.8 1382.4
lme_oneway_new 9 -2787.7 -2745.5 1402.9 41.043 2
pValue
1.2234e-09
p-Value of the likelihood ratio test is close to zero. This indicates that the random effect model is significantly better than the pure fixed-effect model. Since the p-Value of the log_PUB_CAP estimate in the random-effects model is not significant, we can attempt to improve the model.
Two-Way Random effects Model (Mixed-Effect Model)
The two-way random-effects model takes into account the random effect with time as the grouping variable which is individual-invariant. This accounts for any time-specific effect that is not included in the regression. Economically this could account for events that are specific to a year that affect the state private production.
clc lme_twoway = fitlme(publicdata,... ['log_GDP ~ 1 + log_HWY + log_WATER + log_UTIL + log_PVT_CAP +'... 'log_EMP + UNEMP + (1 | STATE) + (1|YR)'],'FitMethod','REML') compare(lme_oneway, lme_twoway)
lme_twoway =
Linear mixed-effects model fit by REML
Model information:
Number of observations 816
Fixed effects coefficients 7
Random effects coefficients 65
Covariance parameters 3
Formula:
Linear Mixed Formula with 8 predictors.
Model fit statistics:
AIC BIC LogLikelihood Deviance
-2876.3 -2829.3 1448.1 -2896.3
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF
{'(Intercept)'} 2.4129 0.15442 15.626 809
{'UNEMP' } -0.0042953 0.0010625 -4.0428 809
{'log_HWY' } 0.08226 0.024747 3.324 809
{'log_WATER' } 0.057152 0.013744 4.1583 809
{'log_UTIL' } -0.090081 0.016155 -5.5759 809
{'log_PVT_CAP'} 0.2212 0.022162 9.981 809
{'log_EMP' } 0.7751 0.024684 31.401 809
pValue Lower Upper
2.6764e-48 2.1098 2.716
5.7872e-05 -0.0063809 -0.0022098
0.00092711 0.033684 0.13084
3.5486e-05 0.030174 0.084131
3.3564e-08 -0.12179 -0.05837
3.3338e-22 0.1777 0.2647
3.7471e-142 0.72664 0.82355
Random effects covariance parameters (95% CIs):
Group: STATE (48 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.093399
Lower Upper
0.075159 0.11606
Group: YR (17 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.015926
Lower Upper
0.010685 0.023737
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.033774 0.032096 0.035541
ans =
THEORETICAL LIKELIHOOD RATIO TEST
Model DF AIC BIC LogLik LRStat deltaDF
lme_oneway 7 -2750.7 -2717.8 1382.4
lme_twoway 10 -2876.3 -2829.3 1448.1 131.59 3
pValue
0
The likelihood ratio test shows that the two-way random effects model is significantly better than the one-way random-effects model.
Multilevel (Hierarchical) Model: STATE nested in REGION
So far we built models that accounted for state-specific contextual information by introducing random effects for each state. This model can be extended to introduce random effects for STATE and REGION. In this example, STATE is nested within REGION. In other words, groups of states form a region and no state-level observation is part of more than one region. This can be done by including a random effect for REGION (9 levels) and a random effect for the interaction term STATE.*REGION (48 levels).
clc lme_hierarchical = fitlme(publicdata,... ['log_GDP ~ 1 + log_HWY + log_WATER + log_UTIL + log_PVT_CAP +'... 'log_EMP + UNEMP + (1|REGION) + (1|STATE:REGION) + (1|YR)'],'FitMethod','REML')
lme_hierarchical =
Linear mixed-effects model fit by REML
Model information:
Number of observations 816
Fixed effects coefficients 7
Random effects coefficients 74
Covariance parameters 4
Formula:
Linear Mixed Formula with 9 predictors.
Model fit statistics:
AIC BIC LogLikelihood Deviance
-2878.2 -2826.5 1450.1 -2900.2
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF
{'(Intercept)'} 2.3928 0.16409 14.582 809
{'UNEMP' } -0.0043974 0.0010682 -4.1168 809
{'log_HWY' } 0.089372 0.024872 3.5933 809
{'log_WATER' } 0.058102 0.013688 4.2446 809
{'log_UTIL' } -0.089943 0.016032 -5.6101 809
{'log_PVT_CAP'} 0.21538 0.022801 9.4461 809
{'log_EMP' } 0.77702 0.025223 30.806 809
pValue Lower Upper
6.2072e-43 2.0707 2.7149
4.2365e-05 -0.0064941 -0.0023007
0.00034626 0.040551 0.13819
2.4433e-05 0.031233 0.084971
2.7777e-08 -0.12141 -0.058473
3.6701e-20 0.17062 0.26013
1.7222e-138 0.72751 0.82653
Random effects covariance parameters (95% CIs):
Group: REGION (9 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.047011
Lower Upper
0.020556 0.10751
Group: STATE:REGION (48 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.082574
Lower Upper
0.065183 0.10461
Group: YR (17 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.016016
Lower Upper
0.010731 0.023903
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.033772 0.032093 0.035537
Regional random effects for UNEMP and HWY with possible correlation
lme_advanced = fitlme(publicdata,... ['log_GDP ~ 1 + log_HWY + log_WATER + log_UTIL + log_PVT_CAP + log_EMP + UNEMP +'... '(1 + log_HWY + UNEMP|REGION) + (1 + log_HWY + UNEMP|STATE:REGION) + (1|YR)'],... 'FitMethod','REML','CovariancePattern',{'Full','Diagonal','Diagonal'}) compare(lme_hierarchical, lme_advanced,'CheckNesting',true)
lme_advanced =
Linear mixed-effects model fit by REML
Model information:
Number of observations 816
Fixed effects coefficients 7
Random effects coefficients 188
Covariance parameters 11
Formula:
Linear Mixed Formula with 9 predictors.
Model fit statistics:
AIC BIC LogLikelihood Deviance
-2999.8 -2915.3 1517.9 -3035.8
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF
{'(Intercept)'} 2.5426 0.42123 6.0362 809
{'UNEMP' } -0.0042169 0.0020824 -2.025 809
{'log_HWY' } 0.079243 0.048999 1.6172 809
{'log_WATER' } 0.035572 0.013372 2.6603 809
{'log_UTIL' } -0.05954 0.017 -3.5024 809
{'log_PVT_CAP'} 0.16467 0.022807 7.22 809
{'log_EMP' } 0.83055 0.026705 31.101 809
pValue Lower Upper
2.4023e-09 1.7158 3.3695
0.043197 -0.0083044 -0.00012929
0.10622 -0.016937 0.17542
0.0079629 0.0093247 0.061819
0.00048641 -0.092909 -0.026171
1.2e-12 0.1199 0.20944
2.6314e-140 0.77813 0.88297
Random effects covariance parameters (95% CIs):
Group: REGION (9 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std' } 1.0807
{'UNEMP' } {'(Intercept)'} {'corr'} -0.07628
{'log_HWY' } {'(Intercept)'} {'corr'} -0.99583
{'UNEMP' } {'UNEMP' } {'std' } 0.0042097
{'log_HWY' } {'UNEMP' } {'corr'} -0.01499
{'log_HWY' } {'log_HWY' } {'std' } 0.1175
Lower Upper
0.6534 1.7874
-0.11649 -0.035823
-0.99589 -0.99577
0.0020541 0.0086273
-0.055524 0.025593
0.070978 0.1945
Group: STATE:REGION (48 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.13535
{'UNEMP' } {'UNEMP' } {'std'} 0.0069407
{'log_HWY' } {'log_HWY' } {'std'} 9.4345e-06
Lower Upper
0.1034 0.17718
0.0051992 0.0092654
NaN NaN
Group: YR (17 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.01954
Lower Upper
0.013218 0.028887
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.028184 0.026673 0.029781
ans =
THEORETICAL LIKELIHOOD RATIO TEST
Model DF AIC BIC LogLik LRStat deltaDF
lme_hierarchical 11 -2878.2 -2826.5 1450.1
lme_advanced 18 -2999.8 -2915.3 1517.9 135.62 7
pValue
0
Table showing Cobb–Douglas Production Function Estimates for different models
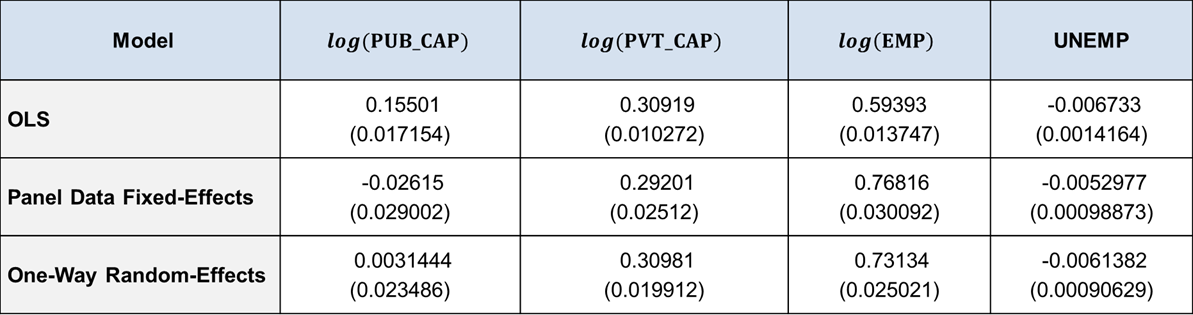
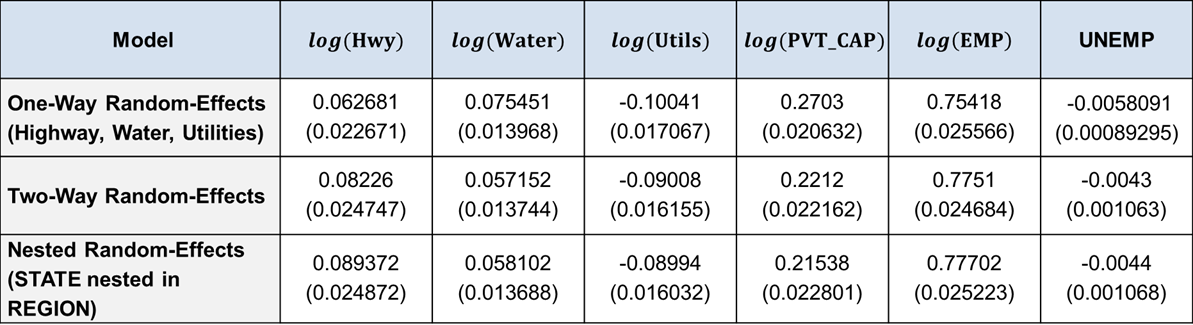
Bibliography
This example is based on the following literature:
[1] Alicia H. Munnell & Leah M. Cook, 1990. "How does public infrastructure affect regional economic performance?," New England Economic Review, Federal Reserve Bank of Boston, issue Sep, pages 11-33.
[2] Econometric Analysis of Panel Data, 5th Edition, Badi H. Baltagi







Comments