PhD Journey Day 15 Stress testing scenario and what to prepare about it

Posted by: admin 3 years, 2 months ago

(Comments)

It turns out that the journey of my PhD brings me to the topic of stress testing. This is a very interesting topic that I am quite passionate about! So the first topic that interests me is about Green economics, move to stress testing, and later about big policy that can be fruitful for the first and second interest. 

Alright so, based on a book that I have read now. There are a couple of steps before we finally move to stress testing. 

The first is to know the macroeconomic analysis and scenario. 

The second is integrating the scenario with internal risk! 

1. Autoregression and moving average modelling
   1. AR (p) analysis 
   2. MA (q) analysis 
   3. ARMA (p,q) analysis 
   4. Box Jenkins Time Series Analysis 
2. Vector Autoregression and Vector Error Correction Modelling
   1. Vector Autoregression and Vector Error Correction Analysis
   2. Vector Autoregression and Vector Error Correction Forecast
   3. Impulse Response Analysis 
3. Global Vector Autoregression modelling
   1. Intro
   2. Global Vector Autoregression analysis 
   3. Global Vector Autoregression Forecast
   4. Generalized Impulse Response Analysis 
4. Stress testing Scenario 
   1. Scenario design
   2. Conditional forecasting 
   3. Bank Stress testing scenario
   4. Macroeconomic modelling and satellite frameworks 

Ok without further a due, let's start! 

Symbol to understand 

• \( X_t \) = random variable at time t 
• \( \chi_t \) = realized value of Xt
• \( x_t \) = vector macroeconomic variable at time t 
• \( \widehat{x}_t \) = estimated vector
• \( x_{t+h|t}\) = h step ahead forecast, given information t 
• \( x^*_{s,t}\) = vector of foreign macro variable for country s time t 
• \( \Delta x_t = x_t - x_{t-1}t \) = Lag 
• L = lag operator
• \( \epsilon_t \) = white noise process
• discrete = not having any connection \( \neq \) continue 
• vector = digital graph or curve based on combination between dot and line (y = a + bc) 
• univariate time series = single observation 
• AR, MA, & ARMA = only for univariate 
• Stationary = constantly move or even not move / swrve at all  

Autoregression and moving average modelling

AR (p) analysis  

Autoregression analysis model 

MA (q) analysis 

ARMA (p,q) analysis 

Box Jenkins Time Series Analysis 

Time to run it in Matlab!

%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Example 2.1                                                                                     %

% Box-Jenkins Analysis                                                                       %

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% File upload

macv=xlsread('Chap2UKmacvar.xlsx');

infl=macv(2:end,14);

% Stationarity ADF test

[h,pvalue]=adftest(infl);

% 1. Specification

Mdl = arima(1,0,0);

% 2. Selection

% 2.1 Estimation

[inflEstMdl inflEstMdlParamCov infllogL]=estimate(Mdl,infl);

% 2.2 Information criteria

[aic,bic] = aicbic(infllogL,2,size(infl,1));

% 3. Model checkDiagnostics

% Residuals

[resinflFit] = infer(inflEstMdl,infl);

% 3.1 Normality

[hNorm0,pNorm0] = lillietest(resinflFit, 'Alpha',0.01);

% 3.2 Ljung-Box Q-test

[hLBQ0,pValueLBQ0] = lbqtest(resinflFit,'Lags',[5,10],'Alpha',0.01);

% Graph residuals

stdr = resinflFit/sqrt(inflEstMdl.Variance);

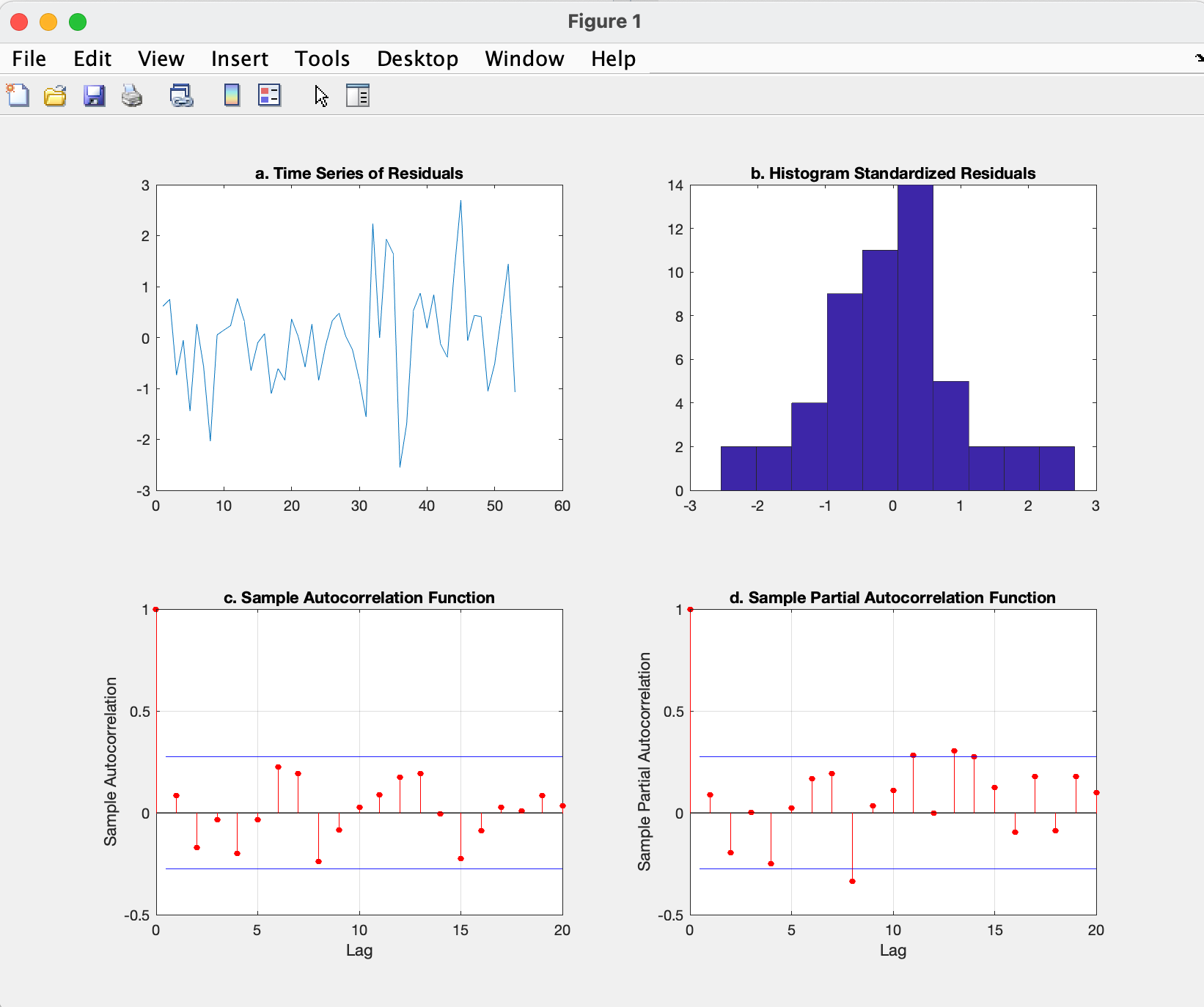
figure; hold('on');

subplot(2,2,1); plot(stdr);

title('a. Time Series of Residuals')

subplot(2,2,2); hist(stdr);

title('b. Histogram Standardized Residuals')

subplot(2,2,3); autocorr(stdr);

title('c. Sample Autocorrelation Function')

subplot(2,2,4); parcorr(stdr);

title('d. Sample Partial Autocorrelation Function')

set(gcf, 'PaperPositionMode', 'manual');

set(gcf, 'PaperUnits', 'centimeters');

set(gcf, 'PaperPosition', [0.5 0.5 28 20]); %left bottom width heigh

set(gcf, 'PaperOrientation', 'landscape');

The result 

Vector Autoregression and Vector Error Correction Modelling

Vector Autoregression and Vector Error Correction Analysis

Before we move to what is vector autoregression, let's take a look at the video that once I created. 

It's pretty funny to see my own note from the past, but definitely, it helps! 

And what is Vector Error correction model, well A vector error correction (VEC) model is a restricted VAR designed for use with nonstationary series that are known to be cointegrated. 

This video explains very well what is Error Correction Model is, from my favourite author Ben Lambert

And part 2

The explanation

How and when using VECM, 

let's say if we get non-stationary variable, then better to regress its first differences (the delta)

\( \Delta Y_t = \delta_0 + \delta_1\Delta X_t + V_t \)

Vt here is the error term 

however, the issue here is, it's only long tun. Also, it will not solve the issue of cointegration where in the long run it will be

\( Y^E = \alpha + \beta X^E \)

So if bot is having cointegration and it means the Y equilibrium in the long run cointegrated with X equilibrium, 

so it makes the differential become

\( Y_t = c + \delta X_t + \delta_2X_{t-1} + \mu Y_{t-1} + V_t \)

The problem here is 

• it does not have economic content because its just about lag formula
• if both y and x are non-stationary then it will make spurious regression or fake regression. 

Based on these two reasons, 

First we take the first different of \( Y_t \)

\( Y_t - Y_{t-1} = c + \delta_1X_t+\delta_2X_{t-1}-(1-\mu) Y_{t-1}\)

after that we get the first difference of Yt, and the YT become stationary. 

The next step is to make Xt become stationary as well

\( \Delta Y_t = \) \(c+ \delta_1X_t -\delta_1X_{t-1} +\delta_1X_{t-1} + \delta_2X_{t-1}-(1-\mu)Y_{t-1}+V_t\)

where \(\delta_1X_{t-1} +\delta_1X_{t-1}\)

\( \Delta Y_t=c+ \delta_1\Delta X_t-\lambda (Y_{t-1}-\alpha -\beta X_{t-1}+V_t\)

Where \( \lambda = 1- \mu\) and \( \beta = \frac{\delta_1+ \delta_2}{1-\mu}\) so it serves short run in the first difference and long run in \( Y_{t-1}-\alpha -\beta X_{t-1}+V_t\)

Vector Autoregression and Vector Error Correction Forecast

Impulse Response Analysis 

Global Vector Autoregression modelling

Intro

Global Vector Autoregression analysis 

Global Vector Autoregression Forecast

Generalized Impulse Response Analysis 

Stress testing Scenario 

Scenario design

Conditional forecasting 

Bank Stress testing scenario

Macroeconomic modelling and satellite frameworks 

• Tags:
• phdjourney

• ← Phd Chapter - Cointegration
• PhD Chapter Matlab vgxset doesnt work →